| 작성자 | 김윤희 |
| 소 감 | 오늘은 인공지능최신기술에서 다룬 semi-supervised learning에 대해서 복습을 진행하였다. 알고 있는 내용들임에도 한 번 더 보니 새롭게 깨달은 것도 많았고, 같이 수강하는 친구들이라 모르는 부분들이나 헷갈리는 부분들을 물어볼 수 있어서 좋았다. |
| 일 시 | 2025. 3. 21. (금) 18:00 ~ 21:00 |
| 장 소 | 미래관 429호 자율주행스튜디오 |
| 참가자 명단 | 신수민, 임혜진, 배세은, 김윤희 (총 4명) |
| 사 진 |  |
Semi-Supervised Learning
- 라벨링 비용을 절감하기 위해서!
- but, unlabeled label은 어떻게 학습을 할까?
Assumptions for Semi-Supervised learning
- Manifold assumptions
- semi-SL이 아니여도 일반적인 딥러닝에서 기본적으로 깔고가는 가정일 것
- 차원이 낮으니까 의미있는 feature들만 살리는 효과?
- PCA, t-sne같은 차원축소는 마지막에 시각화를 위해 사용하는 것이지 semi-SL에서 방법론으로 사용하진 않음
- → 고차원 데이터를 저차원 공간에서 표현할 수 있다 (원본 데이터의 차원을 줄여주능거임)
- Smoothness assumption
- → 다차원 공간 상에서 가까운 거리에 있는 샘플들은 label이 같을 것이다.
- Cluster assumption
- → 데이터는 클러스터를 형성할 것이며, 같은 클러스터에 속한 샘플은 같은 label을 공유할 것이다
Consistency Regularization
motive: 같은 데이터에 작은 변화를 주더라도 예측이 일관되어야 한다.
unlabeled 데이터인 고양이에 다른 두가지 augmentation(label-preserving augmentation)을 준 후 예측값은 동일해야한다! (고양인지 개잉ㄴ지는 모르겠지만 일단 비슷해야함)
- 파이-model
- phi ~= perturbation

- labeling 경우
- 위 과정인 CE loss를 통해 학습 + Consistency R loss 를 진행
- unlabeling 경우
- ex) [0.8, 0.2] , [0.5, 0.5] → 0.3 **2 + 0.3 **2 (loss)
- Consistency R loss 를 사용
- 단점
- 현재 시점의 prediction만 사용함
- 학습 초반에는 가중치가 랜덤한 상태로 초기화 → prediction 가 불안정⇒ 얘를 해결하기위해서 Temporal emsembling
- prediction 2 개가 다 불안정하다면 target(consistency loss)도 불안정해짐
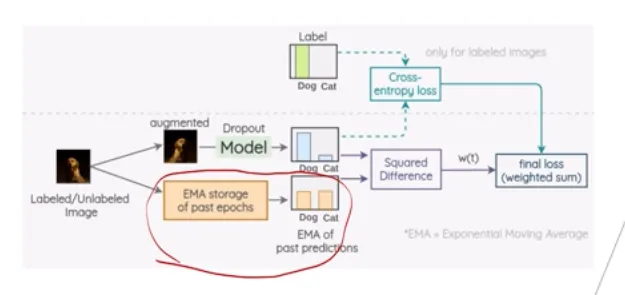
- Temporal EnseblingEMA (Exponential moving average)
- 이전 epoch에서 얻은 데이터의 prediction 값을 누적하여 사용
- 이전 시점의 영향은 점점 낮추면서, 현재 시점의 영향은 상대적으로 높이는 방향으로
- augmentation을 1 번만 진행하여 나온 prediction 값 하나랑 EMA로 업데이트된 prediction 값 하나의 차이를 이용하여 Consistency R 의 loss를 계산
- 단점 → 모든 데이터의 prediction을 저장해야하므로 메모리 사용량이 크다!
- Mean teacher
- 데이터 prediction이 아니라 모델 가중치에 EMA를 적용
- Teacher-sutedent framework
- Student model: gradient desent를 통해 학습 (unstable)
- teacher model: Student model의 가중치를 EMA로 누적→ stable, smoothed target 제공
- (이미 학습이 완료된 teacher가 아님)
- 적은 가중치로도 teacher를 흉내내는 student 모델을 만들고 싶운거임
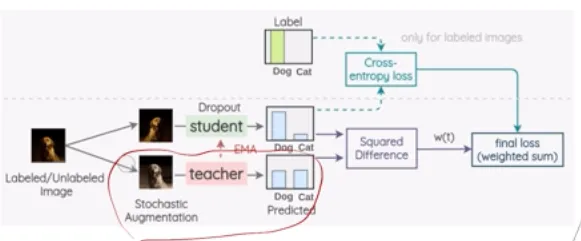
- 두 번의 augmentation을 진행
- student model은 CE loss로 update
- teacher는 직접적으로 CE나 consistency R loss를 사용하는게 아님
- student의 가중치 ema로 update!
'윤희' 카테고리의 다른 글
| [호붕싸 모각코 6차] CA-MoE: Channel-Adapted MoE for Incremental Weather Forecasting 논문 리뷰 (0) | 2025.03.31 |
|---|---|
| [호붕싸 모각코 5차] beakjoon 2225. 합분해 (0) | 2025.03.24 |
| [호붕싸 모각코 3주차] Unimodal Representation (0) | 2025.03.17 |
| [호붕싸 모각코 2주차] 실전프로젝트 문제 다시풀기 (0) | 2025.03.14 |
| [호붕싸 모각코 1주차] Leetcode 62. Unique Paths, 72. Edit Distance (0) | 2025.03.10 |